Schriftlich Dividieren Mit Rest Aufgaben

Mathematik > Zahlenlehre und Rechengesetze

Schriftlich Dividieren mit Komma

Inhaltsverzeichnis:

In diesem Kapitel befassen wir uns mit der schriftlichen Division. Das ist eine einfache Methode, mit der du große Zahlen ohne Taschenrechner dividieren kannst. Im Folgenden werden wir eine Beispielaufgabe zur schriftlichen Division durchrechnen und die Regeln für die schriftliche Segmentation erklären.

Methode

Methode

Hier klicken zum Ausklappen

Die Grundlage für dieses Kapitel bildet das Wissen über die Division. Falls du nicht mehr genau weißt, wie man dividiert, dann schau noch einmal im Lerntext zum Thema Division nach. Dort findest du nochmal eine Erklärung zur schriftlichen Division.

Schriftliche Partition

Du kennst bereits die Division. Das schriftliche Dividieren unterscheidet sich nicht von der Division an sich, sondern ist nur eine Methode, mit der du große Zahlen einfacher dividieren kannst, ohne den Taschenrechner verwenden zu müssen. Du kannst likewise damit dann schriftlich rechnen. Schauen wir uns hierzu eine Beispielaufgabe an:

Beispiel

Beispiel

Hier klicken zum Ausklappen

Aufgabenstellung: Dividiere $1596 \; $ durch $fourteen$.

Um die beiden Zahlen dividieren zu können, schreiben wir sie erst einmal nebeneinander:

$1596 \; : \; xiv \; =$

Im nächsten Schritt schauen wir, ob die erste Zahl der $1596$ durch dice $14$ teilbar ist. Die $1$ ist nicht durch $14$ teilbar, also nehmen wir dice zweite Zahl auch dazu:

Der erste Schritt der Beispieldivision.

$xv \; : \; 14$ ergibt $1$, Rest $1$. Den Rest schreiben wir, wie auf dem Bild ersichtlich, unter die Division der beiden Zahlen und die Lösung hinter das Gleichheitszeichen:

Der zweite Schritt der Beispieldivision.

Da sich dice entstandene $1$ nicht durch $xiv$ teilen lässt, ziehen wir die $nine$ herunter und die and so entstandene $19$ durch $14$ teilen:

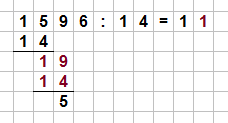
Der dritte Schritt der Beispieldivision.

Das Ergebnis der Sectionalisation von $19$ durch $14$ ist $1$. Diese schreiben wir neben die $1$ der ersten Partition. Der Remainder, $v$, wird wieder für den nächsten Schritt benötigt. Wir ziehen die $vi$ hinter dice $five$ und erhalten $56$, welche wir wieder durch $14$ teilen.

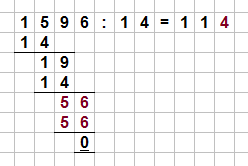
Der vierte Schritt der Beispieldivision.

Die Zahl $56$ ist durch $14$ teilbar, es ergibt sich $4$. Diese schreiben wir neben die beiden Einsen und erhalten das Ergebnis der Division, nämlich $114$.

Um jetzt zu überprüfen, ob das Ergebnis stimmt, kannst du das entstandene Ergebnis $114$ mit $xiv$ multiplizieren. Es sollte dann das Ergebnis $1596$ herauskommen.

Schriftliches Dividieren - Der Rest

Bei der schriftlichen Sectionalisation, wie auch bei der "normalen" Division, kann ein Rest übrig bleiben. Dieser wird dann nach dem Ergebnis dargestellt. Dice folgende Abbildung zeigt, wie die schriftliche Division mit Residuum funktioniert:

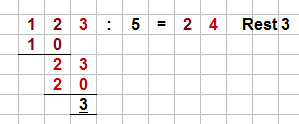
Eine schriftliche Division mit Residue.

Schriftliches Dividieren - Dice Probe

Um jetzt zu überprüfen, ob das errechnete Ergebnis stimmt, macht man eine Probe. Bei dieser wird das Ergebnis der Division, as well der Quotient, mit dem Divisor multipliziert. Es sollte der Dividend entstehen.

Achtung: Wenn dein Quotient jedoch einen Remainder hatte, dann musst du den Remainder noch zum Ergebnis dazu addieren. In unserer Abbildung wäre das besides:

$(24 \cdot 5) \; + \; three \;=\; 123$

Merke

Merke

Hier klicken zum Ausklappen

Die schriftliche Division ist eine Methode zum einfachen Dividieren großer Zahlen.

Bei der schriftlichen Division wird der Rest hinter das Ergebnis geschrieben.

Bei der Probe wird derQuotient mit dem Divisor multipliziert und der Remainder dazu addiert.

Zur Vertiefung dieses Themas schau auch noch einmal in dice Aufgaben zur schriftlichen Division! Dabei wünschen wir dir viel Spaß und Erfolg!

Source: https://www.studienkreis.de/mathematik/schriftlich-dividieren-rest/

Posted by: gravesexcums.blogspot.com

Share this post