How To Graph The Time Domain Of A Highpass Filter

How to Plot the Frequency Response of a Filter

This article shows how to plot the frequency response of the filters that I draw in my articles on filter design. Plotting this kind of frequency response should non be confused with the spectral density estimation of measured signals, which can be (much) more involved. For the specific case of a filter, nevertheless, the frequency response tells you exactly how each frequency is altered. The example code is in Python, as usual, but the methodology is applicative for whatever programming language or plotting tool.

Time and Frequency Representation

The principal functioning that will become you from the time domain to the frequency domain is the Discrete Fourier Transform (DFT). In practice, you'll typically use the Fast Fourier Transform (FFT) , which is an efficient algorithm for computing the DFT.

A crucially important indicate is that simply computing the FFT of the filter is not enough. Equally an case, Figure ane shows a low-pass filter, equally presented in How to Create a Elementary Low-Pass Filter, both in the time domain (left) and in the frequency domain (correct).

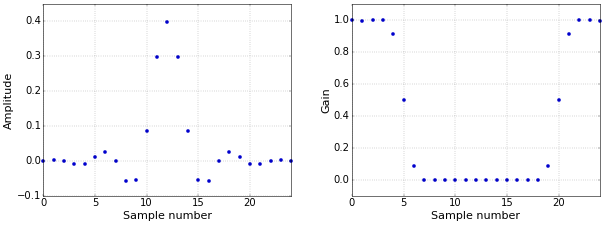Figure 1. Time domain (left) and frequency domain (right) representation of a filter. Effigy ane. Time domain (left) and frequency domain (right) representation of a filter.

The dots in the frequency domain plot are exactly the result of the FFT, only, by themselves, they don't requite yous a clear pic of the true frequency response. There are at least three reasons for this:

The frequency response of a detached-fourth dimension (or digital) filter is continuous, even though the Fourier transform is a finite number of points.
The response that is plotted is typically from 0 Hz to half of the sampling rate. Still, the bodily outcome of the FFT contains a mirror of this in its second half (in the more general example of filters with complex coefficients this is no longer truthful, just I'll keep that for a future commodity).
The plot has a linear scale, while frequency plots more often than not accept a logarithmic calibration (in dB).

Every bit a start footstep towards the typical frequency response plots that you are probably more familiar with, Figure two shows only the first half of the FFT, in dB. I take an article on the normalized frequency that is used on the X axis, if you are curious.

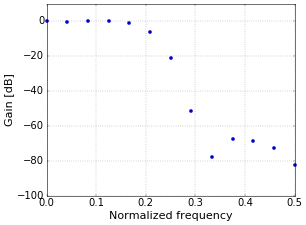Figure 2. Frequency response of filter in dB.

Continuous Frequency Response

The dots in Figure 2 are samples of the complete frequency response. Still, the actual frequency response of the filter is, of course, continuous, since it has an exactly defined effect on every frequency that you put through the filter. To show the continuous frequency response of the filter, some more work is needed. The way to do this is to "pad with zeros". You increment the length of the time signal, typically to a power of ii such every bit 1024 (the ability of two is simply for the FFT algorithm). The reason that y'all are allowed to do this, is that calculation zeros does not change the filter, since the zeros take no result. Nevertheless, the result of the FFT of this longer point, still only samples of the true response, will be smooth when plotted in a graph. The result of padding with zeros to a length of 1024 samples is shown in Effigy three.

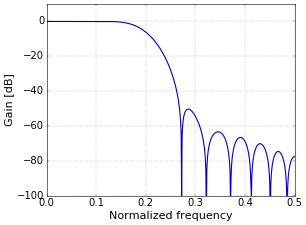Figure 3. Frequency response of padded filter.

The plot of Figure iii is exactly how I commonly present frequency response plots. Python code that creates this plot follows in the next section.

Python Lawmaking

                                                                  from                        __future__                        import                        sectionalization                        import                        numpy                        as                        np                        import                        matplotlib.pyplot                        as                        plt   fc                        =                        0.2                        # Cutoff frequency as a fraction of the sampling rate (in (0, 0.5)).                        Due north                        =                        25                        # Number of coefficients.                        L                        =                        1024                        # Length of frequency response.                        # Compute sinc filter with Hamming window.                        northward                        =                        np.arange                        (N)                        h                        =                        np.sinc                        (                        2                        * fc *                        (n -                        (Northward -                        1                        )                        /                        ii                        )                        )                        * np.hamming                        (N)                        h /=                        np.sum                        (h)                        # Pad filter with zeros.                        h_padded                        =                        np.zeros                        (L)                        h_padded[                        0                        : N]                        =                        h                        # Compute frequency response; only continue first half.                        H                        =                        np.abs                        (np.fft.fft                        (h_padded)                        )                        [                        0                        : 50 //                        2                        +                        1                        ]                        # Plot frequency response (in dB).                        plt.figure                        (                        )                        plt.plot                        (np.linspace                        (                        0                        ,                        0.5                        ,                        len                        (H)                        )                        ,                        20                        * np.log10                        (H)                        )                        plt.xlabel                        (                        'Normalized frequency'                        )                        plt.ylabel                        (                        'Gain [dB]'                        )                        plt.ylim                        (                        [-100                        ,                        x                        ]                        )                        plt.grid                        (                        )                        plt.show                        (                        )